Over the holidays, I participated in Kaggle’s Packing Santa’s Sleigh challenge. Developing a solution was a lot of fun but I didn’t have the chance to post about it until now.

The challenge consisted of packing one million presents of varying sizes into Santa’s sleigh. The sleigh had a fixed width and length but could grow as tall as necessary to fit the presents. The goal was to pack the presents with the smallest height and in delivery order. The evaluation metric was a score that increased with height and the “distance” presents were packed from the optimal order.

That second constraint, packing in delivery order, was both a blessing and a curse. It was a blessing because it meant that the solution didn’t have to consider packing all one million presents at the same time. However, it was also a curse because it limited the freedom to re-order presents to achieve an optimal packing.

I hadn’t solved a problem like this before so I started off doing some research. I eventually decided that the problem was essentially a bin packing problem with the ordering constraint making it more like a cutting stock problem. A Kaggle forum post referenced an excellent paper by Jukka Jylanki on two dimensional bin packing that was really helpful.

With that initial research done, I started out by implementing a simple shelf algorithm. I packed the presents in delivery order using a simple Guillotine partitioning scheme. This result achieved a score close to that of the provided example solution (which used a similar approach). I added code to do height compaction and got a score good enough to fall in the middle of the leaderboard.

After this initial success, I spent a few days pursuing a queue based algorithm that added empty space back as the bottom of each packed present was reached. This required implementing a defragmentation algorithm based on finding a minimal cover of a set of overlapping rectilinear rectangles. I had a lot of fun implementing an algorithm but the queue approach performed worse than the initial shelf approach. Unfortunately, I ventured on this tangent during the last week of the competition.

At this point, I realized that the most important thing was to pack each shelf as densely as possible. I experimented with different methods but began to run out of time. My final solution essentially consisted of:

• Selecting the next N presents, in delivery order, that would fill a shelf if packed optimally.
• Packing these presents in largest to smallest order.
• Checking to see if the packed presents had gaps in delivery order.
• If not, commit to the packing and perform height compaction based on the heights of the presents packed on the previous shelf.
• If there were gaps, use a binary-ish search algorithm to find the subset of presents that could be packed in decreasing size order that didn’t result in any gaps.

This algorithm worked well but was very slow. As a result, I didn’t have time to investigate other approaches. Although I’ve learned this lesson before, this is further evidence that I need to start Kaggle competitions sooner. My final score was within 16% of the winning result and was good enough to put me in 92nd place out of 362 teams. I’m happy with that but hope to place higher in future competitions.

As an added challenge, I decided to implement my solution in Julia, a new technical computing language that has been getting a lot of attention. Like R, Julia’s design is heavily influence by LISP, one of my favorite programming languages. This was my first experience with Julia and, overall, I enjoyed it. It’s ability to dynamically compile to native machine code was the feature I was most interested as I’ve had runtime speed issues with R and Python while working on past Kaggle competitions. Julia seemed to perform well but I don’t have a baseline to compare it to. Unlike Common Lisp implementations that I’ve used in the past, Julia doesn’t appear to use late-binding for compiled routines. This meant that any time I updated a routine all callers of that routine also needed to be re-compiled. The essentially devolved into an edit-compile-run development cycle reminiscent of static languages. But, Julia is still in early days so perhaps this will change (or, equally likely, I wasn’t doing it right).

As an additional challenge, I also implemented a solution viewer in Processing. Here’s a screenshot,

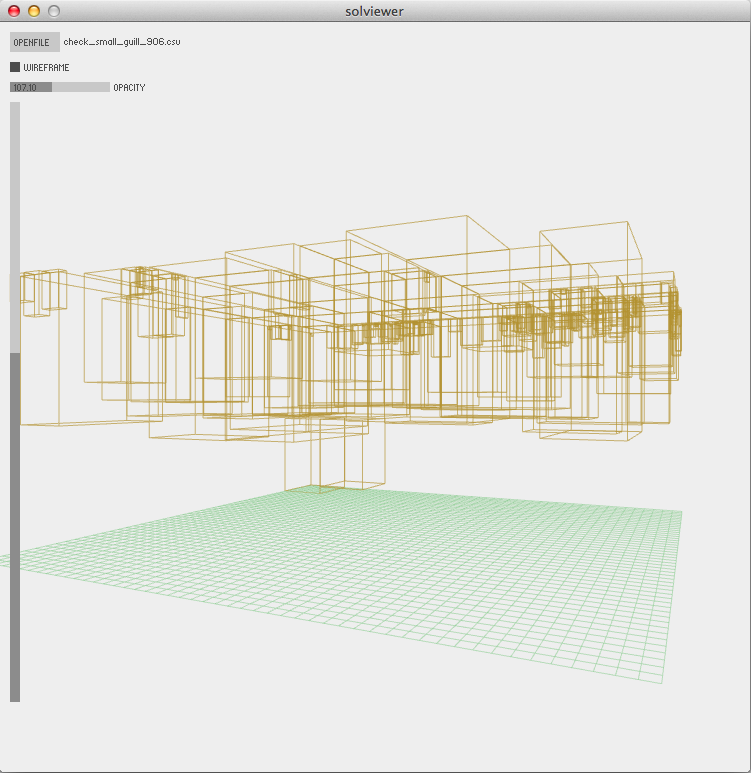
I’ve been looking for an excuse to learn Processing and this seemed like an ideal opportunity. The viewer was only able to visualize solutions with thousands of presents. However, this was sufficient during early development using small subsets of presents.

Wrapping up, I had a lot of fun with this challenge. I enjoyed learning about computational geometry problems and algorithms. Using Julia was a fun experiment and I look forward to using it to solve other problems. Building the Processing solution viewer was also fun. This is why I like doing Kaggle competitions. They provide opportunities to learn new tools, topics, etc, as well as improve one’s skill. In this regard, it really doesn’t matter where you end up in the leaderboard (but I still want to do better next time).

The source code for my final solution and Processing solution viewer are available on GitHub. The repository also includes additional code that I wrote while investigating other approaches, including the minimal rectangle cover algorithm (see the routine mincoverrects() in the file experimental.jl).