DSGeek

January 29, 2015

Skewing Around, Part 3

In parts 1 and 2 , I described how I used the AMS and HyperLogLog online algorithms to estimate the frequency distribution of values in multiple integer sequences. I was doing this for a friend that needed a compute and space efficient way to analyze thousands of such streams.

Although the solution I came up with in Part 2 worked, it didn’t express the “skew” in human understandable terms like “20% of the values accounted for 80% of the occurrences”. Challenge accepted.

In the last post, I explained that an integer stream of length $O$ with an equal number of occurrences of $N$ values will have a minimum surprise number of,

$$ \begin{aligned} S_{min} &= \frac{O^2}{N} \end{aligned} $$

And that this can be combined with the estimated surprise number to create a scaled “skew” metric $R$ that is comparable between different streams,

$$ R = \frac{\hat{S}}{S_{min}} $$\/

Now, consider a stream where proportion \$q\$ of the values account for proportion \$p\$ of the occurrences. With some simplifying assumptions, the surprise number for this stream will be,

$$ \begin{aligned} S_{pq} &= \sum_{i}^{qN} \left(\frac{pO}{qN}\right)^2 + \sum_{j}^{(1-q)N} \left(\frac{(1-p)O}{(1-q)N}\right)^2\\ &= \frac{(pO)^2}{qN} + \frac{((1-p)O)^2}{(1-q)N}\\ \end{aligned} $$

The resulting $R$ metric will be,

$$ \begin{aligned} R &= \frac{S_{pq}}{S_{min}}\\ &= \frac{\frac{(pO)^2}{qN} + \frac{((1-p)O)^2}{(1-q)N}}{S_{min}}\\ &= \frac{\frac{(pO)^2}{qN} + \frac{((1-p)O)^2}{(1-q)N}}{\frac{O^2}{N}}\\ &= \frac{p^2}{q} + \frac{(1-p)^2}{(1-q)}\\ &= \frac{p^2(1-q)}{q(1-q)} + \frac{q(1-)^2)}{q(1-q)}\\ &= \frac{p^2(1-q) + q(1 - 2p + p^2)}{q(1-q)}\\ &= \frac{p^2 - p^2q + q - 2pq + p^2q}{q(1-q)}\\ &= \frac{p^2 + q - 2pq}{q(1-q)}\\ &= \frac{p^2 + q - 2pq + (q^2 - q^2)}{q(1-q)}\\ &= \frac{(p^2 - 2pq + q^2) + q - q^2}{q(1-q)}\\ &= \frac{(p-q)^2 + q(1-q)}{q(1-q)}\\ &= \frac{(p-q)^2}{q(1-q)} + 1\\ \end{aligned} $$

Expressing this in terms of the estimated ratio described in the last post leads to,

$$ \begin{aligned} R &= \frac{\hat{S}}{S_{min}} \approx \frac{(p-q)^2}{q(1-q)} + 1\\ \end{aligned} $$

Now, lets substitute $R$ with a new metric $R^{\prime} = \tilde{R} - 1$,

$$ \begin{aligned} R^{\prime}_s &\approx \frac{(p-q)^2}{q(1-q)}\\ R^{\prime} q(1-q) &\approx (p-q)^2\\ \sqrt{R^{\prime} q(1-q)} &\approx p-q\\ p &\approx q + \sqrt{R^{\prime} q(1-q)}\\ \end{aligned} $$

Since this equation has two unknowns, there are many solutions of $p$ and $q$ for a given $R^{\prime}$. For example, $\tilde{R} = 3.25$ has an infinite number of possible solutions including: ${p=.9, q=.25},{p=.8, q=.2}, {p=.6,q=.15}$. The following figure illustrates this,

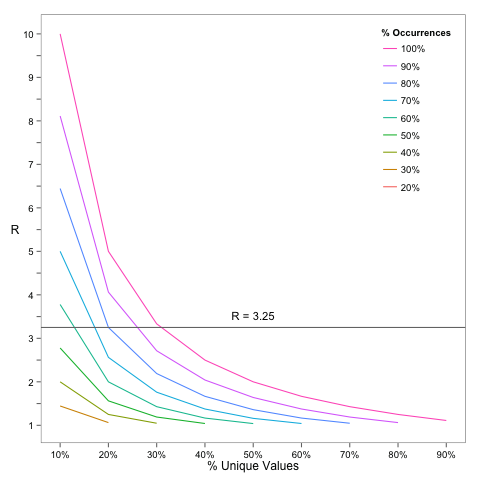
However, as the figure suggests, an upper bound on $q$ can be found by setting $p <= 1$.

$$ \begin{aligned} q + \sqrt{R^{\prime} q(1-q)} &<= 1\\ \sqrt{R^{\prime} q(1-q)} &<= (1-q)\\ R^{\prime} q(1-q) &<= (1-q)^2\\ R^{\prime} q &<= (1-q)\\ R^{\prime} &<= \frac{(1-q)}{q}\\ R^{\prime} &<= \frac{1}{q} - 1\\ R^{\prime} + 1 &<= \frac{1}{q}\\ \end{aligned} $$

Recalling the definition of $R^{\prime}$,

$$ \begin{aligned} R - 1 + 1 &<= \frac{1}{q}\\ R &<= \frac{1}{q}\\ q &<= \frac{1}{R}\\ \end{aligned} $$

This means that the upper bound on the percentage of skewed values is the reciprocal of the estimated $R$. Cool!

Unfortunately, with both $p$ and $q$ unknown and only one equation, this was as far as I could take this. However, the upper bound and family of curves for given values of $p$ were enough for my friend to do what he wanted.

This was a fun project. I got to see first hand that although probabilistic online algorithms sacrifice accuracy for efficiency, they can still perform well enough to get the job done!

Tags: MachineLearning , Streams